Skip to main content

Constraint and Penalty

caution

This document is out-dated. Go back to latest page

We explain jm.Constraint at Introduction of JijModeling. However, JijModeling has more features to build more wide range of mathematical models. In this note, we will explain another class, jm.CustomPenaltyTerm, and the more features in jm.Constraint. The figure below shows the differences between jm.Constraint and jm.CustomPenaltyTerm.

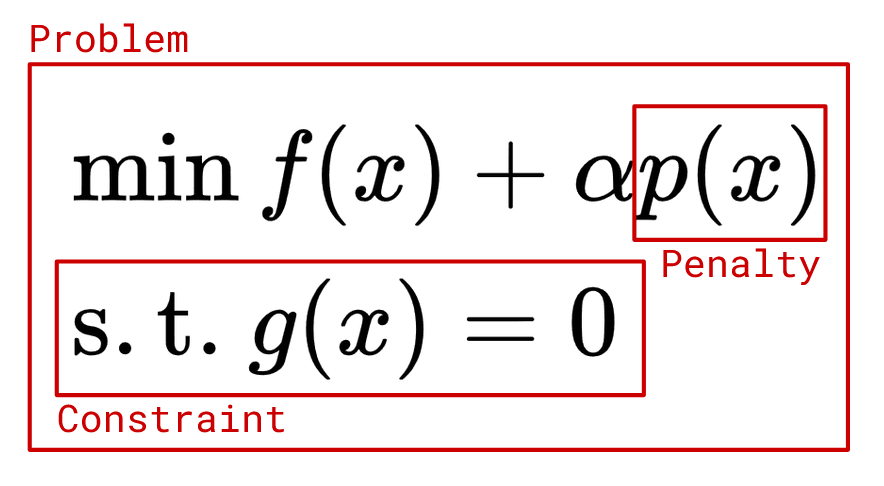
jm.Constraint defines the constraints in the mathematical model. On the other hand, jm.CustomPenaltyTerm defines penalty terms that are directly added to the Objective function.

Let us see what jm.CustomPenaltyTerm is first.

Custom penalty term​

jm.CustomPenaltyTerm is the interface to define custom penalty terms by ourselves. The interface is provided to control QUBO directly. Unlike jm.Constraint, JijZept does not calculate the violation of it.

There are two basic usages for this interface:

  1. Soft Constraint
  2. User Custom Penalty

Soft Constraints are the constraints that do not have to be satisfied but would be better to be satisfied. You can use jm.CustomPenaltyTerm to define this Soft Constraint.

Another usage is user custom penalty. This is an advanced usage of jm.CustomPenaltyTerm. When the constraint is too complicated to use for annealing, sometimes, we can convert this constraint into a simple form to modify the QUBO directly. However, we would like to check the constraint violation of the original form of the constraint.

We can use jm.CustomPenaltyTerm almost the same as jm.Constraint. The code below shows how to use jm.CustomPenaltyTerm.

import jijmodeling as jm

# define variables
N = jm.Placeholder('N')
K = jm.Placeholder('K')
A = jm.Placeholder('A', ndim=1)
x = jm.BinaryVar('x', shape=(N, K))
i = jm.Element('i', belong_to=(0, K))
u = jm.Element('u', belong_to=(0, N))

problem = jm.Problem('penalty_sample')
problem += jm.CustomPenaltyTerm('one hot penalty',  jm.sum(u,A[u] * (jm.sum(i,x[u, i]) - 1)**2))
problem += jm.Constraint('one hot', jm.sum(i,x[u, i]) == 1, forall=u)
problem
Problem:penalty_samplemin⁡0s.t.one hot∑i=0K−1xu,i=1∀u∈{0,…,N−1}penalty termsone hot penalty∑u=0N−1Au⋅(∑i=0K−1xu,i−1)2wherex2-dim binary variable\begin{array}{cccc} \text{Problem:} & \text{penalty\_sample} & & \\ & & \min \quad \displaystyle 0 & \\ \text{s.t.} & & & \\ & \text{one hot} & \displaystyle \sum_{i = 0}^{K - 1} x_{u, i} = 1 & \forall u \in \left\{0,\ldots,N - 1\right\} \\ \text{penalty terms} & & & \\ & \text{one hot penalty} & \displaystyle \sum_{u = 0}^{N - 1} A_{u} \cdot \left(\sum_{i = 0}^{K - 1} x_{u, i} - 1\right)^{2} & \\ \text{{where}} & & & \\ & x & 2\text{-dim binary variable}\\ \end{array}

The form of the second argument of jm.CustomPenaltyTerm is not the equation. It should be the form of the term which you would like to add to the Objective function.